Day 14: Restroom Redoubt
Megathread guidelines
- Keep top level comments as only solutions, if you want to say something other than a solution put it in a new post. (replies to comments can be whatever)
- You can send code in code blocks by using three backticks, the code, and then three backticks or use something such as https://topaz.github.io/paste/ if you prefer sending it through a URL
FAQ
- What is this?: Here is a post with a large amount of details: https://programming.dev/post/6637268
- Where do I participate?: https://adventofcode.com/
- Is there a leaderboard for the community?: We have a programming.dev leaderboard with the info on how to join in this post: https://programming.dev/post/6631465
C
Solved part 1 without a grid, looked at part 2, almost spit out my coffee. Didn’t see that coming!
I used my visualisation mini-library to generate video with ffmpeg, stepped through it a bit, then thought better of it - this is a programming puzzle after all!
So I wrote a heuristic to find frames low on entropy (specifically: having many robots in the same line of column), where each record-breaking frame number was printed. That pointed right at the correct frame!
It was pretty slow though (.2 secs or such) because it required marking spots on a grid.
I noticed the Christmas tree was neatly tucked into a corner, concluded that wasn’t an accident, and rewrote the heuristic to check for a high concentration in a single quadrant.Reverted this because the tree-in-quadrant assumption proved incorrect for other inputs. Would’ve been cool though!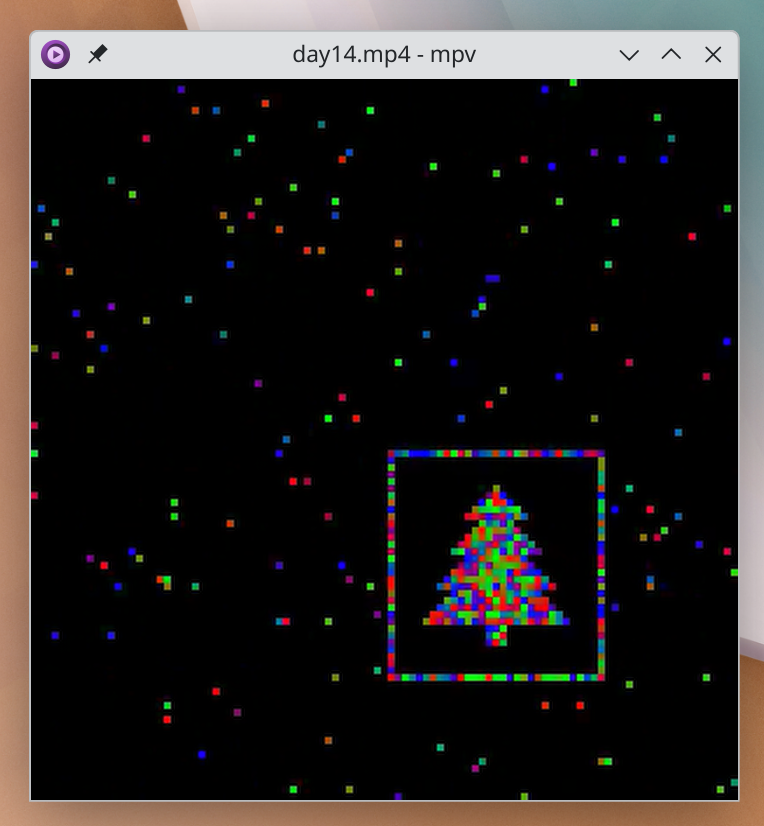
Code
#include "common.h" #define SAMPLE 0 #define GW (SAMPLE ? 11 : 101) #define GH (SAMPLE ? 7 : 103) #define NR 501 int main(int argc, char **argv) { static char g[GH][GW]; static int px[NR],py[NR], vx[NR],vy[NR]; int p1=0, n=0, sec, i, x,y, q[4]={}, run; if (argc > 1) DISCARD(freopen(argv[1], "r", stdin)); for (; scanf(" p=%d,%d v=%d,%d", px+n,py+n, vx+n,vy+n)==4; n++) assert(n+1 < NR); for (sec=1; !SAMPLE || sec <= 100; sec++) { memset(g, 0, sizeof(g)); memset(q, 0, sizeof(q)); for (i=0; i<n; i++) { px[i] = (px[i] + vx[i] + GW) % GW; py[i] = (py[i] + vy[i] + GH) % GH; g[py[i]][px[i]] = 1; if (sec == 100) { if (px[i] < GW/2) { if (py[i] < GH/2) q[0]++; else if (py[i] > GH/2) q[1]++; } else if (px[i] > GW/2) { if (py[i] < GH/2) q[2]++; else if (py[i] > GH/2) q[3]++; } } } if (sec == 100) p1 = q[0]*q[1]*q[2]*q[3]; for (y=0; y<GH; y++) for (x=0, run=0; x<GW; x++) if (!g[y][x]) run = 0; else if (++run >= 10) goto found_p2; } found_p2: printf("14: %d %d\n", p1, sec); return 0; }TypeScript
Part 2 was a major curveball for sure. I was expecting something like the grid size and number of seconds multiplying by a large amount to make iterative solutions unfeasible.
First I was baffled how we’re supposed to know what shape we’re looking for exactly. I just started printing out cases where many robots were next to each other and checked them by hand and eventually found it. For my input the correct picture looked like this:
The Christmas tree

Later it turned out that a much simpler way is to just check for the first time none of the robots are overlapping each other. I cannot say for sure if this works for every input, but I suspect the inputs are generated in such a way that this approach always works.
The code
import fs from "fs"; type Coord = {x: number, y: number}; type Robot = {start: Coord, velocity: Coord}; const SIZE: Coord = {x: 101, y: 103}; const input: Robot[] = fs.readFileSync("./14/input.txt", "utf-8") .split(/[\r\n]+/) .map(row => /p=(-?\d+),(-?\d+)\sv=(-?\d+),(-?\d+)/.exec(row)) .filter(matcher => matcher != null) .map(matcher => { return { start: {x: parseInt(matcher[1]), y: parseInt(matcher[2])}, velocity: {x: parseInt(matcher[3]), y: parseInt(matcher[4])} }; }); console.info("Part 1: " + safetyFactor(input.map(robot => calculatePosition(robot, SIZE, 100)), SIZE)); // Part 2 // Turns out the Christmas tree is arranged the first time none of the robots are overlapping for (let i = 101; true; i++) { const positions = input.map(robot => calculatePosition(robot, SIZE, i)); if (positions.every((position, index, arr) => arr.findIndex(pos => pos.x === position.x && pos.y === position.y) === index)) { console.info("Part 2: " + i); break; } } function calculatePosition(robot: Robot, size: Coord, seconds: number): Coord { return { x: ((robot.start.x + robot.velocity.x * seconds) % size.x + size.x) % size.x, y: ((robot.start.y + robot.velocity.y * seconds) % size.y + size.y) % size.y }; } function safetyFactor(positions: Coord[], size: Coord): number { const midX = Math.floor(size.x / 2); const midY = Math.floor(size.y / 2); let quadrant0 = 0; // Top-left let quadrant1 = 0; // Top-right let quadrant2 = 0; // Bottom-left let quadrant3 = 0; // Bottom-right for (const {x,y} of positions) { if (x === midX || y === midY) { continue; } if (x < midX && y < midY) { quadrant0++; } else if (x > midX && y < midY) { quadrant1++; } else if (x < midX && y > midY) { quadrant2++; } else if (x > midX && y > midY) { quadrant3++; } } return quadrant0 * quadrant1 * quadrant2 * quadrant3; }Checking for no overlaps is an interesting one. Intuitively I’d expect that to happen more often due to the low density, but as you say perhaps it’s deliberate.
Haskell, alternative approach
The x and y coordinates of robots are independent. 101 and 103 are prime. So, the pattern of x coordinates will repeat every 101 ticks, and the pattern of y coordinates every 103 ticks.
For the first 101 ticks, take the histogram of x-coordinates and test it to see if it’s roughly randomly scattered by performing a chi-squared test using a uniform distrobution as the basis. [That code’s not given below, but it’s a trivial transliteration of the formula on wikipedia, for instance.] In my case I found a massive peak at t=99.
Same for the first 103 ticks and y coordinates. Mine showed up at t=58.
You’re then just looking for solutions of t = 101m + 99, t = 103n + 58 [in this case]. I’ve a library function, maybeCombineDiophantine, which computes the intersection of these things if any exist; again, this is basic wikipedia stuff.
day14b ls = let rs = parse ls size = (101, 103) positions = map (\t -> process size t rs) [0..] -- analyse x coordinates. These should have period 101 xs = zip [0..(fst size)] $ map (\rs -> map (\(p,_) -> fst p) rs & C.count & chi_squared (fst size)) positions xMax = xs & sortOn snd & last & fst -- analyse y coordinates. These should have period 103 ys = zip [0..(snd size)] $ map (\rs -> map (\(p,_) -> snd p) rs & C.count & chi_squared (snd size)) positions yMax = ys & sortOn snd & last & fst -- Find intersections of: t = 101 m + xMax, t = 103 n + yMax ans = do (s,t) <- maybeCombineDiophantine (fromIntegral (fst size), fromIntegral xMax) (fromIntegral (snd size), fromIntegral yMax) pure $ minNonNegative s t in trace ("xs distributions: " ++ show (sortOn snd xs)) $ trace ("ys distributions: " ++ show (sortOn snd ys)) $ trace ("xMax = " ++ show xMax ++ ", yMax = " ++ show yMax) $ trace ("answer could be " ++ show ans) $ ansVery nice!
I should add - it’s perfectly possible to draw pictures which won’t be spotted by this test, but in this case as it happens the distributions are exceedingly nonuniform at the critical point.
Very cool, taking a statistical approach to discern random noise from picture.
Thanks. It was the third thing I tried - began by looking for mostly-symmetrical, then asked myself “what does a christmas tree look like?” and wiring together some rudimentary heuristics. When those both failed (and I’d stopped for a coffee) the alternative struck me. It seems like a new avenue into the same diophantine fonisher that’s pretty popular in these puzzles - quite an interesting one.
This day’s puzzle is clearly begging for some inventive viaualisations.
Haskell
Part 2 could be improved significantly now that I know what to look for, but this is the (very inefficient) heuristic I eventually found the answer with.
Solution
import Control.Arrow import Data.Char import Data.List import Data.Map qualified as Map import Data.Maybe import Text.Parsec (w, h) = (101, 103) readInput :: String -> [((Int, Int), (Int, Int))] readInput = either (error . show) id . parse (robot `endBy` newline) "" where robot = (,) <$> (string "p=" >> coords) <*> (string " v=" >> coords) coords = (,) <$> num <* char ',' <*> num num = read <$> ((++) <$> option "" (string "-") <*> many1 digit) runBots :: [((Int, Int), (Int, Int))] -> [[(Int, Int)]] runBots = transpose . map botPath where botPath (p, (vx, vy)) = iterate (incWrap w vx *** incWrap h vy) p incWrap s d = (`mod` s) . (+ d) safetyFactor :: [(Int, Int)] -> Int safetyFactor = product . Map.fromListWith (+) . map (,1) . mapMaybe quadrant where cx = w `div` 2 cy = h `div` 2 quadrant (x, y) | x == cx || y == cy = Nothing | otherwise = Just (x `div` (cx + 1), y `div` (cy + 1)) render :: [(Int, Int)] -> [String] render bots = let counts = Map.fromListWith (+) $ map (,1) bots in flip map [0 .. h - 1] $ \y -> flip map [0 .. w - 1] $ \x -> maybe '.' intToDigit $ counts Map.!? (x, y) isImage :: [String] -> Bool isImage = (> 4) . length . filter hasRun where hasRun = any ((> 3) . length) . filter head . group . map (/= '.') main = do positions <- runBots . readInput <$> readFile "input14" print . safetyFactor $ positions !! 100 let (Just (t, image)) = find (isImage . snd) $ zip [0 ..] $ map render positions print t mapM_ putStrLn imageHaskell. For part 2 I just wrote 10000 text files and went through them by hand. I quickly noticed that every 103 seconds, an image started to form, so it didn’t take that long to find the tree.
Code
import Data.Maybe import Text.ParserCombinators.ReadP import qualified Data.Map.Strict as M type Coord = (Int, Int) type Robot = (Coord, Coord) int :: ReadP Int int = fmap read $ many1 $ choice $ map char $ '-' : ['0' .. '9'] coord :: ReadP Coord coord = (,) <$> int <*> (char ',' *> int) robot :: ReadP Robot robot = (,) <$> (string "p=" *> coord) <*> (string " v=" *> coord) robots :: ReadP [Robot] robots = sepBy robot (char '\n') simulate :: Coord -> Int -> Robot -> Coord simulate (x0, y0) t ((x, y), (vx, vy)) = ((x + t * vx) `mod` x0, (y + t * vy) `mod` y0) quadrant :: Coord -> Coord -> Maybe Int quadrant (x0, y0) (x, y) = case (compare (2*x + 1) x0, compare (2*y + 1) y0) of (LT, LT) -> Just 0 (LT, GT) -> Just 1 (GT, LT) -> Just 2 (GT, GT) -> Just 3 _ -> Nothing freqs :: (Foldable t, Ord a) => t a -> M.Map a Int freqs = foldr (\x -> M.insertWith (+) x 1) M.empty solve :: Coord -> Int -> [Robot] -> Int solve grid t = product . freqs . catMaybes . map (quadrant grid . simulate grid t) showGrid :: Coord -> [Coord] -> String showGrid (x0, y0) cs = unlines [ [if (x, y) `M.member` m then '#' else ' ' | x <- [0 .. x0]] | let m = M.fromList [(c, ()) | c <- cs] , y <- [0 .. y0] ] main :: IO () main = do rs <- fst . last . readP_to_S robots <$> getContents let g = (101, 103) print $ solve g 100 rs sequence_ [ writeFile ("tree_" ++ show t) $ showGrid g $ map (simulate g t) rs | t <- [0 .. 10000] ]This one was wild. At first I started visualling it but wasn’t seeing anything. I went up to almost 80 iterations before giving up. I then went with the “no overlapping points thing” but didn’t think that was working for me either.
It was iteration 7,753. f’s sake man.
I used the a modulo operation and an if check to skip ahead to the final state. It was also tricky b/c the grid is larger than I could get my console to work with.
F#
(just the important bits)
type Velocity = Point2I [<Struct>]type Robot = {Position:Point2I; Velocity:Velocity} type Boundary = {MaxX:int; MaxY: int} let move ticks boundary robot = let newX = ((robot.Position.X + (robot.Velocity.X * ticks)) % boundary.MaxX) |> fun x -> if x < 0 then boundary.MaxX + x else x let newY = ((robot.Position.Y + (robot.Velocity.Y * ticks)) % boundary.MaxY) |> fun x -> if x < 0 then boundary.MaxY + x else x { robot with Position = {X = newX; Y = newY} } let toQuadrantScore boundary robots = let removeX = ((boundary.MaxX |> float) / 2.0) |> int let removeY = ((boundary.MaxY |> float) / 2.0) |> int ((0,0,0,0), robots) ||> Seq.fold(fun (a,b,c,d) robot -> if robot.Position.X < removeX && robot.Position.Y < removeY then (a+1,b,c,d) else if robot.Position.X > removeX && robot.Position.Y < removeY then (a,b+1,c,d) else if robot.Position.X < removeX && robot.Position.Y > removeY then (a,b,c+1,d) else if (robot.Position.X > removeX && robot.Position.Y > removeY) then (a,b,c,d+1) else (a,b,c,d) ) |> fun (a,b,c,d) -> a*b*c*d let part1impl boundary ticks robots = robots |> Seq.map(move ticks boundary) |> toQuadrantScore boundary let part1 input = (read input parse) |> part1impl {MaxX = 101; MaxY = 103 } 100 let part2 input = let robots = (read input parse) |> Array.ofSeq let boundary = {MaxX = 101; MaxY = 103 } // I'll steal the no overlapping robots approach // since I'll just be iterating through, I'll do batches of 100 numbers each in parallel and then draw it // up to 100 batches [0..100] |> List.find (fun batch -> try seq {0..100} |> Seq.pick (fun t -> // I could use PSeq here, but I'd have to remove the console stuff as the locking and fighting for the console in parallel really slows it let ticks = batch * 100 + t Console.Clear() Console.SetCursorPosition(0,0) Console.Write(ticks) let count = robots |> PSeq.map (move ticks boundary) |> PSeq.distinctBy _.Position |> PSeq.length if count = 500 then ... write to file, consoleI got so lucky that “no overlapping” worked for mine. It was a very undefined problem.
Yeah I don’t know how long I would have tried to solve that on my own. I was starting to wonder if I did something wrong because I read seeing patterns every 80 iterations or so
Someone did use that periodic pattern to cut down on the search space.
I saw that. I think it sort of made sense haha. There’s a reason I’m not in statistics or analytics lol
Haskell
I solved part two interactively, I’m not very happy about it
Reveal Code
import Control.Arrow import Data.Bifunctor hiding (first, second) import Control.Monad import qualified Data.List as List import qualified Data.Set as Set import qualified Data.Map as Map import qualified Data.Maybe as Maybe parse :: String -> [((Int, Int), (Int, Int))] parse = map (break (== ' ') >>> second (drop 1) >>> join bimap (drop 2) >>> join bimap (break (== ',')) >>> join bimap (second (drop 1)) >>> join bimap (join bimap read)) . filter (/= "") . lines moveRobot ((px, py), (vx, vy)) t = (px + t * vx, py + t * vy) constrainCoordinates (mx, my) (px, py) = (px `mod` mx, py `mod` my) coordinateConstraints = (101, 103) robotQuadrant (mx, my) (px, py) | px > middleX && py < middleY = Just 1 -- upper right | px > middleX && py > middleY = Just 2 -- lower right | px < middleX && py > middleY = Just 3 -- lower left | px < middleX && py < middleY = Just 4 -- upper left | otherwise = Nothing where middleX = (mx `div` 2) middleY = (my `div` 2) countQuadrants (q1, q2, q3, q4) 1 = (succ q1, q2, q3, q4) countQuadrants (q1, q2, q3, q4) 2 = (q1, succ q2, q3, q4) countQuadrants (q1, q2, q3, q4) 3 = (q1, q2, succ q3, q4) countQuadrants (q1, q2, q3, q4) 4 = (q1, q2, q3, succ q4) part1 = map (flip moveRobot 100 >>> constrainCoordinates coordinateConstraints) >>> map (robotQuadrant coordinateConstraints) >>> Maybe.catMaybes >>> foldl (countQuadrants) (0, 0, 0, 0) >>> \ (a, b, c, d) -> a * b * c * d showMaybe (Just i) = head . show $ i showMaybe Nothing = ' ' buildRobotString robotMap = [ [ showMaybe (robotMap Map.!? (x, y)) | x <- [0..fst coordinateConstraints] ] | y <- [0..snd coordinateConstraints]] part2 rs t = map (flip moveRobot t >>> constrainCoordinates coordinateConstraints) >>> flip zip (repeat 1) >>> Map.fromListWith (+) >>> buildRobotString $ rs showConstellation (i, s) = do putStrLn (replicate 49 '#' ++ show i ++ replicate 49 '#') putStrLn $ s main = do f <- getContents let i = parse f print $ part1 i let constellations = map (id &&& (part2 i >>> List.intercalate "\n")) . filter ((== 86) . (`mod` 103)) $ [0..1000000] mapM_ showConstellation constellations print 7502Rust
Part 2 was very surprising in that it had a very vague requirement: “Find christmas tree!”. But my idea of finding the first round where no robots overlap turned out to just work when printing the map, so that was nice. I’m glad I did not instead start looking for symmetric patterns, because the christmas tree map is not symmetric at all.
Solution
use euclid::default::*; use regex::Regex; fn parse(input: &str) -> Vec<(Point2D<i32>, Vector2D<i32>)> { let re = Regex::new(r"p=(\d+),(\d+) v=(-?\d+),(-?\d+)").unwrap(); re.captures_iter(input) .map(|cap| { let (_, [p0, p1, v0, v1]) = cap.extract(); ( Point2D::new(p0.parse().unwrap(), p1.parse().unwrap()), Vector2D::new(v0.parse().unwrap(), v1.parse().unwrap()), ) }) .collect() } const ROOM: Size2D<i32> = Size2D::new(101, 103); const TIME: i32 = 100; fn part1(input: String) { let robots = parse(&input); let new_pos: Vec<Point2D<i32>> = robots.iter() .map(|&(p, v)| (p + v * TIME).rem_euclid(&ROOM)) .collect(); assert_eq!(ROOM.width % 2, 1); assert_eq!(ROOM.height % 2, 1); let mid_x = ROOM.width / 2; let mid_y = ROOM.height / 2; let mut q = [0u32; 4]; for p in new_pos { use std::cmp::Ordering::*; match (p.x.cmp(&mid_x), p.y.cmp(&mid_y)) { (Less, Less) => q[0] += 1, (Greater, Less) => q[1] += 1, (Less, Greater) => q[2] += 1, (Greater, Greater) => q[3] += 1, _ => {} }; } let prod = q[0] * q[1] * q[2] * q[3]; println!("{prod}"); } fn print_map(map: &[Vec<bool>]) { for row in map { for p in row { if *p { print!("#") } else { print!(".") } } println!(); } println!(); } fn part2(input: String) { let mut robots = parse(&input); let mut map = vec![vec![false; ROOM.width as usize]; ROOM.height as usize]; for i in 1.. { let mut overlap = false; for (p, v) in &mut robots { *p = (*p + *v).rem_euclid(&ROOM); if map[p.y as usize][p.x as usize] { // Found two robots on the same spot, // which is used as a heuristic for detecting the easter egg. overlap = true; } else { map[p.y as usize][p.x as usize] = true; } } if !overlap { print_map(&map); println!("Round: {i}"); break; } for row in &mut map { row.fill(false); } } } util::aoc_main!();Also on github
Python
I was very confused when I saw the second part. I was like “how the fuck am I supposed now how that shape will exactly look like?” I looked a couple of initial shapes all of which looked sufficiently random. So I constructed x and y marginal distributions of the robots to impose some non-symmetry conditions.
My initial attempt was to just require maximum of x marginal should be at the centre but the sneaky bastards apparently framed the tree and tree was shorter than I expected (realised this only later) so that did not return any hits. I played around a bit and settled for: most of the maximums of x marginal should be near the centre and y marginal should be asymmetric. I still had to play around with the thresholds for these a bit because initially there was a couple of shapes (some repeating every 100 cycles or so) that satisfied my requirements (I had a part which actually outputted found shapes to a text file but then removed that in the final code). So it wasn’t %100 free of manual labour but I can say mostly…
import numpy as np from pathlib import Path from collections import Counter cwd = Path(__file__).parent def parse_input(file_path): with file_path.open("r") as fp: robot_info = fp.readlines() _split = lambda x,p: [int(x.split(' ')[p].split(',')[0].split('=')[-1]), int(x.split(' ')[p].split(',')[-1])] robot_pos = np.array([_split(x, 0) for x in robot_info]) robot_vel = np.array([_split(x, 1) for x in robot_info]) return robot_pos, robot_vel def solve_problem1(file_name, nrows, ncols, nmoves): robot_pos, robot_vel = parse_input(Path(cwd, file_name)) final_pos = robot_pos + nmoves*robot_vel final_pos = [(x[0]%ncols, x[1]%nrows) for x in list(final_pos)] pos_counts = Counter(final_pos) coords = np.array(list(pos_counts.keys()))[:,::-1] #x is cols, y is rows coords = tuple(coords.T) grid = np.zeros((nrows, ncols), dtype=int) grid[coords] += list(pos_counts.values()) counts = [np.sum(grid[:nrows>>1, :ncols>>1]), np.sum(grid[:nrows>>1, -(ncols>>1):]), np.sum(grid[-(nrows>>1):, :ncols>>1]), np.sum(grid[-(nrows>>1):, -(ncols>>1):])] return int(np.prod(counts)) def solve_problem2(file_name, nrows, ncols): robot_pos, robot_vel = parse_input(Path(cwd, file_name)) grid = np.zeros((nrows, ncols), dtype=object) # update all positions in a vectorised manner final_positions = robot_pos[None, :, :] + np.arange(1,10000)[:,None,None]*robot_vel[None,:,:] final_positions[:,:,0] = final_positions[:,:,0]%ncols final_positions[:,:,1] = final_positions[:,:,1]%nrows for s in range(final_positions.shape[0]): grid[:,:] = 0 final_pos = map(tuple, tuple(final_positions[s,:,:])) pos_counts = Counter(final_pos) coords = np.array(list(pos_counts.keys()))[:,::-1] #x is cols, y is rows coords = tuple(coords.T) grid[coords] += list(pos_counts.values()) xmarg = np.sum(grid, axis=0) tops = set(np.argsort(xmarg)[::-1][:10]) p_near_center = len(tops.intersection(set(range((ncols>>1)-5, (ncols>>1) + 6))))/10 ymarg = np.sum(grid, axis=1) ysym = 1 - abs(ymarg[:nrows>>1].sum() - ymarg[nrows>>1:].sum())/ymarg.sum() if p_near_center>0.5 and ysym<0.8: return s+1Nim
Part 1: there’s no need to simulate each step, final position for each robot is
(position + velocity * iterations) modulo grid
Part 2: I solved it interactively: Maybe I just got lucky, but my input has certain pattern: after 99th iteration every 101st iteration looking very different from other. I printed first couple hundred iterations, noticed a pattern and started looking only at “interesting” grids. It took 7371 iterations (I only had to check 72 manually) to reach an easter egg.type Vec2 = tuple[x,y: int] Robot = object pos, vel: Vec2 var GridRows = 101 GridCols = 103 proc examine(robots: seq[Robot]) = for y in 0..<GridCols: for x in 0..<GridRows: let c = robots.countIt(it.pos == (x, y)) stdout.write if c == 0: '.' else: char('0'.ord + c) stdout.write '\n' stdout.flushFile() proc solve(input: string): AOCSolution[int, int] = var robots: seq[Robot] for line in input.splitLines(): let parts = line.split({' ',',','='}) robots.add Robot(pos: (parts[1].parseInt,parts[2].parseInt), vel: (parts[4].parseInt,parts[5].parseInt)) block p1: var quads: array[4, int] for robot in robots: let newX = (robot.pos.x + robot.vel.x * 100).euclmod GridRows newY = (robot.pos.y + robot.vel.y * 100).euclmod GridCols relRow = cmp(newX, GridRows div 2) relCol = cmp(newY, GridCols div 2) if relRow == 0 or relCol == 0: continue inc quads[int(relCol>0)*2 + int(relRow>0)] result.part1 = quads.foldl(a*b) block p2: if GridRows != 101: break p2 var interesting = 99 var interval = 101 var i = 0 while true: for robot in robots.mitems: robot.pos.x = (robot.pos.x + robot.vel.x).euclmod GridRows robot.pos.y = (robot.pos.y + robot.vel.y).euclmod GridCols inc i if i == interesting: robots.examine() echo "Iteration #", i, "; Do you see an xmas tree?[N/y]" if stdin.readLine().normalize() == "y": result.part2 = i break interesting += intervalJ
Had to actually render output! What is this “user interface” of which you speak?
J doesn’t have meaningful identifiers for system interfaces built into the core language because why would you ever do that. It’s all routed through the “foreign conjunction”
!:. There are aliases in the library, likefread, but if the documentation gives a list of all of them, I haven’t found it. We’re doing 1980 style system calls by number here.1 !: 2iswrite(), sox (1 !: 2) 2writesx(which must be a list of characters) tostdout.(6 !: 3) yissleepforyseconds.It’s inefficient to compute, but I looked for low spots in the mean distance between robots to find the pattern for part 2. The magic numbers (11 and 101) were derived by staring at the entire series for a little bit.
load 'regex' data_file_name =: '14.data' raw =: cutopen fread data_file_name NB. a b sublist y gives elements [a..a+b) of y sublist =: ({~(+i.)/)~"1 _ parse_line =: monad define match =: 'p=(-?[[:digit:]]+),(-?[[:digit:]]+) v=(-?[[:digit:]]+),(-?[[:digit:]]+)' rxmatch y 2 2 $ ". y sublist~ }. match ) initial_state =: parse_line"1 > raw 'positions velocities' =: ({."2 ; {:"2) initial_state steps =: 100 size =: 101 103 step =: (size & |) @: + travel =: step (steps & *) quadrant =: (> & (<. size % 2)) - (< & (<. size % 2)) final_quadrants =: quadrant"1 @: travel"1 quadrant_ids =: 4 2 $ 1 1 _1 1 1 _1 _1 _1 result1 =: */ +/"1 quadrant_ids -:"1/ positions final_quadrants velocities render =: monad define |: 'O' (<"1 y)} size $ '.' ) pair_distances =: monad : 'y (| @: j./ @: -/"1)/ y' loop =: dyad define positions =. positions step"1 (velocities * x) for_i. i. 1000 do. time_number =. x + i * y mean_distance =. (+/ % #) , pair_distances positions if. mean_distance < 50 do. (render positions) (1!:2) 2 (": time_number, mean_distance) (1!:2) 2 (6!:3) 1 end. if. mean_distance < 35 do. break. end. positions =. positions step"1 (velocities * y) end. time_number result2 =: 11 loop 101Dart
Took far too long to work out a really stupidly simple method of finding the tree – I ended up just checking the first height*width time slots to find when the most bots appear in any given row/column. The framing around the Christmas tree accidentally made this foolproof :-). Add a bit of Chinese Remainder Theorem and we’re golden. (edit: forgot to mention that it’s Dart code)
import 'dart:math'; import 'package:collection/collection.dart'; import 'package:more/more.dart'; List<List<Point<num>>> getBots(List<String> lines) { var bots = lines .map((e) => RegExp(r'(-?\d+)') .allMatches(e) .map((m) => int.parse(m.group(0)!)) .toList()) .map((p) => [Point<num>(p[0], p[1]), Point<num>(p[2], p[3])]) .toList(); return bots; } // Solve system of congruences using the Chinese Remainder Theorem int crt(int r1, int m1, int r2, int m2) { int inv = m1.modInverse(m2); int solution = (r1 + m1 * ((r2 - r1) % m2) * inv) % (m1 * m2); return (solution + (m1 * m2)) % (m1 * m2); // Ensure the result is positive } void moveBy(List<List<Point<num>>> bots, int t, int w, int h) { for (var b in bots) { b.first += b.last * t; b.first = Point(b.first.x % w, b.first.y % h); } } part1(List<String> lines, [width = 11, height = 7]) { var bots = getBots(lines); moveBy(bots, 100, width, height); var w = width ~/ 2, h = height ~/ 2; var quads = Multiset.fromIterable( bots.map((b) => (b.first.x.compareTo(w), b.first.y.compareTo(h)))); return [(-1, -1), (-1, 1), (1, -1), (1, 1)] .map((k) => quads[k]) .reduce((s, t) => s * t); } part2(List<String> lines, [width = 101, height = 103]) { var bots = getBots(lines); var t = 0; int rmax = 0, cmax = 0, rt = 0, ct = 0; while (t < width * height) { t += 1; moveBy(bots, 1, width, height); var r = Multiset.fromIterable(bots.map((e) => e.first.x)).counts.max; var c = Multiset.fromIterable(bots.map((e) => e.first.y)).counts.max; if (r > rmax) (rmax, rt) = (r, t); if (c > cmax) (cmax, ct) = (c, t); } t = crt(rt, width, ct, height); bots = getBots(lines); moveBy(bots, t, width, height); // printGrid(height, width, bots); return t; }Haskell
Spent a lot of time trying to find symmetric quadrants. In the end made an interactive visualization and found that a weird pattern appeared on iterations (27 + 101k) and (75 + 103k’). Put those congruences in an online Chinese remainder theorem calculator and go to the answer:
x ≡ 8006 (mod 101*103)import Data.Bifunctor import Data.Char import qualified Data.Set as S import Data.Functor import Data.List import Control.Monad import Text.ParserCombinators.ReadP import Data.IORef bounds = (101, 103) parseInt :: ReadP Int parseInt = (*) <$> option 1 (char '-' $> (-1)) <*> (read <$> munch1 isDigit) parseTuple = (,) <$> parseInt <*> (char ',' *> parseInt) parseRow = (,) <$> (string "p=" *> parseTuple) <*> (string " v=" *> parseTuple) parse = fst . last . readP_to_S (endBy parseRow (char '\n')) move t (x, y) (vx, vy) = bimap (mod (x + vx * t)) (mod (y + vy * t)) bounds getQuadrant :: (Int, Int) -> Int getQuadrant (x, y) | x == mx || y == my = 0 | otherwise = case (x > mx, y > my) of (True, True) -> 1 (True, False) -> 2 (False, True) -> 3 (False, False) -> 4 where (mx, my) = bimap (`div` 2) (`div` 2) bounds step (x, y) (vx, vy) = (,(vx, vy)) $ bimap (mod (x + vx)) (mod (y + vy)) bounds main = do p <- parse <$> readFile "input14" print . product . fmap length . group . sort . filter (/=0) . fmap (getQuadrant . uncurry (move 100)) $ p let l = iterate (fmap (uncurry step)) p current <- newIORef 0 actions <- lines <$> getContents forM_ actions $ \a -> do case a of "" -> modifyIORef current (+1) "+" -> modifyIORef current (+1) "-" -> modifyIORef current (subtract 1) n -> writeIORef current (read n) pos <- readIORef current putStr "\ESC[2J" -- clear screen print pos visualize $ fst <$> l !! pos visualize :: [(Int, Int)] -> IO () visualize pos = do let p = S.fromList pos forM_ [1..(snd bounds)] $ \y -> do forM_ [1..(fst bounds)] $ \x -> do putChar $ if S.member (x, y) p then '*' else '.' putChar '\n'Uiua
Ok, so part one wasn’t too hard, and since uiua also takes negative values for accessing arrays, I didn’t even have to care about converting my modulus results (though I did later for part two).
I’m a bit conflicted about the way I detected the quadrants the robots are in, or rather the way the creation of the mask-array happens. I basically made a 11x7 field of 0’s, then picked out each quadrant and added 1-4 respectively. Uiua’s group (⊕) function then takes care of putting all the robots in separate arrays for each quadrant. Simple.For part two, I didn’t even think long before I came here to see other’s approaches. The idea to look for the first occurrence where no robots’ positions overlapped was my starting point for what follows.
Example input stuff
Run with example input here
$ p=0,4 v=3,-3 $ p=6,3 v=-1,-3 $ p=10,3 v=-1,2 $ p=2,0 v=2,-1 $ p=0,0 v=1,3 $ p=3,0 v=-2,-2 $ p=7,6 v=-1,-3 $ p=3,0 v=-1,-2 $ p=9,3 v=2,3 $ p=7,3 v=-1,2 $ p=2,4 v=2,-3 $ p=9,5 v=-3,-3 . PartOne ← ( # &rs ∞ &fo "input-14.txt" ⊜(↯2_2⋕regex"-?\\d+")≠@\n. ≡(⍜⌵(◿11_7)+°⊟⍜⊡₁×₁₀₀) ↯⟜(▽×°⊟)7_11 0 ⍜↙₃(⍜≡↙₅+₁⍜≡↘₆+₂) ⍜↘₄(⍜≡↙₅+₃⍜≡↘₆+₄) /×≡◇⧻⊕□-₁⊸(⊡:)⍉ ) PartTwo ← ( # &rs ∞ &fo "input-14.txt" ⊜(↯2_2⋕regex"-?\\d+")≠@\n. 0 # number of seconds to start at 0_0 ⍢(◡(≡(⍜⌵(◿11_7)+°⊟⍜⊡₁×):)◌ ◿[11_7]≡+[11_7] ⊙+₁ | ≠⊙(⧻◴)⧻.) ⊙◌◌ -₁ ) &p "Day 14:" &pf "Part 1: " &p PartOne &pf "Part 2: " &p PartTwo
Now on to the more layered approach of how I got my solution.
In my case, there’s two occasions of non-overlapping positions before the christmas tree appears.
I had some fun trying to get those frames and kept messing up with going back and forth between 7x11 vs 103x101 fields, often forgetting to adjust the modulus and other parts, so that was great.In the end, I uploaded my input to the online uiua pad to make visualizing possible frames easier since uiua is able to output media if the arrays match a defined format.
Try it out yourself with your input
- Open the uiua pad with code here
- Replace the
0in the first line with your solution for part two - If necessary, change the name of the file containing your input
- Drag a file containing your input onto the pad to upload it and run the code
- An image should be displayed
I used this code to find the occurrence of non-overlapping positions (running this locally):
&rs ∞ &fo "input-14.txt" ⊜(↯2_2⋕regex"-?\\d+")≠@\n. 0 # number of seconds to start at 0_0 ⍢(◡(≡(⍜⌵(◿101_103)+°⊟⍜⊡₁×):)◌ ◿[101_103]≡+[101_103] ⊙+₁ | ≠⊙(⧻◴)⧻.) ⊙◌◌ -₁Whenever a new case was found, I put the result into the code in the online pad to check the generated image, and finally got this at the third try:

C#
using System.Text.RegularExpressions; namespace aoc24; [ForDay(14)] public partial class Day14 : Solver { [GeneratedRegex(@"^p=(-?\d+),(-?\d+) v=(-?\d+),(-?\d+)$")] private static partial Regex LineRe(); private List<(int X, int Y, int Vx, int Vy)> robots = []; private int width = 101, height = 103; public void Presolve(string input) { var data = input.Trim(); foreach (var line in data.Split("\n")) { if (LineRe().Match(line) is not { Success: true } match ) { throw new InvalidDataException($"parse error: ${line}"); } robots.Add(( int.Parse(match.Groups[1].Value), int.Parse(match.Groups[2].Value), int.Parse(match.Groups[3].Value), int.Parse(match.Groups[4].Value) )); } } public string SolveFirst() { Dictionary<(bool, bool), int> quadrants = []; foreach (var robot in robots) { int x = (robot.X + 100 * (robot.Vx > 0 ? robot.Vx : robot.Vx + width)) % width; int y = (robot.Y + 100 * (robot.Vy > 0 ? robot.Vy : robot.Vy + height)) % height; if (x == width/2 || y == height/2) continue; var q = (x < width / 2, y < height / 2); quadrants[q] = quadrants.GetValueOrDefault(q, 0) + 1; } return quadrants.Values.Aggregate((a, b) => a * b).ToString(); } private int CountAdjacentRobots(HashSet<(int, int)> all_robots, (int, int) this_robot) { var (x, y) = this_robot; int count = 0; for (int ax = x - 1; all_robots.Contains((ax, y)); ax--) count++; for (int ax = x + 1; all_robots.Contains((ax, y)); ax++) count++; for (int ay = y - 1; all_robots.Contains((x, ay)); ay--) count++; for (int ay = y + 1; all_robots.Contains((x, ay)); ay++) count++; return count; } public string SolveSecond() { for (int i = 0; i < int.MaxValue; ++i) { HashSet<(int, int)> end_positions = []; foreach (var robot in robots) { int x = (robot.X + i * (robot.Vx > 0 ? robot.Vx : robot.Vx + width)) % width; int y = (robot.Y + i * (robot.Vy > 0 ? robot.Vy : robot.Vy + height)) % height; end_positions.Add((x, y)); } if (end_positions.Select(r => CountAdjacentRobots(end_positions, r)).Max() > 10) { return i.ToString(); } } throw new ArgumentException(); } }







